Support-Vector-Machines sind ein klassisches und effektives Verfahren im maschinellen Lernen, das sich insbesondere in der Klassifikation bewährt hat. Im Vergleich zu Künstlichen Neuronalen Netzen verfolgen SVMs einen fundamental anderen Ansatz. Während neuronale Netze durch das Zusammenspiel vieler verbundener Neuronen lernen, konzentriert sich eine SVM darauf, die Datenpunkte einerseits geometrisch zu trennen und dabei eine klare, optimale Trennlinie zu finden.
In diesem Artikel vergleichen wir die Funktionsweise von SVMs mit der von neuronalen Netzen und zeigen auf, wann der Einsatz von SVMs sinnvoller ist.
Grundlegender Unterschied: Entscheidungsfindung
Der wesentliche Unterschied zwischen SVMs und neuronalen Netzen liegt in der Art, wie Entscheidungen getroffen werden.
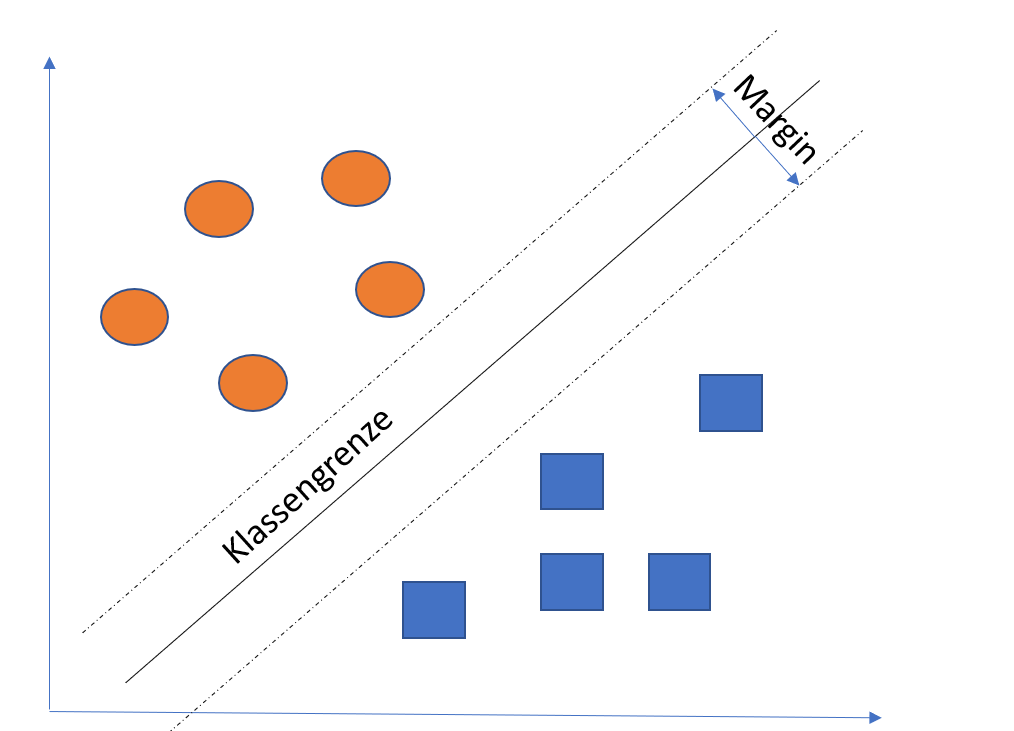
- SVM: Eine Support-Vector-Machine arbeitet darauf hin, eine optimale Trennlinie (in höheren Dimensionen als „Hyperplane“ bezeichnet) zu finden, die zwei Klassen von Datenpunkten trennt. Das Besondere dabei ist, dass die SVM nicht nur irgendeine Trennlinie wählt, sondern jene, die den größtmöglichen Abstand (den sogenannten Margin) zu den nächstgelegenen Datenpunkten beider Klassen hat. Dies führt in der Regel zu einem robusteren Modell, das gut verallgemeinert.
- Neuronale Netze: Künstliche neuronale Netze hingegen nutzen ein komplexes System aus miteinander verbundenen „Neuronen“ in verschiedenen Schichten. Das Netz lernt, indem es die Verbindungen (Gewichte) zwischen diesen Neuronen so anpasst, dass die Ausgabewerte möglichst gut mit den gewünschten Klassifikationen übereinstimmen. Diese nichtlineare Struktur erlaubt es neuronalen Netzen, sehr komplexe Zusammenhänge in den Daten zu erkennen.
Datenanforderungen und Generalisierung
- SVM: Eine der Stärken der SVM liegt darin, dass sie auch bei kleineren Datensätzen sehr gut funktioniert, besonders wenn die Anzahl der Merkmale (Features) hoch ist. Die SVM ist zudem robust gegen Overfitting, da sie darauf optimiert ist, den Abstand zwischen der Trennlinie und den Datenpunkten zu maximieren. Dadurch kann sie gut auf unbekannte Daten generalisieren, selbst wenn das Trainingsset relativ klein ist.
- Neuronale Netze: Neuronale Netze benötigen in der Regel eine große Menge an Trainingsdaten, um die vielen Parameter (Gewichte) effektiv zu lernen. Wenn die Datenmenge zu gering ist, besteht die Gefahr, dass das Modell sich zu stark an die Trainingsdaten anpasst (Overfitting) und bei neuen Daten schlecht performt. Sie brillieren jedoch bei großen, komplexen Datensätzen, wie es etwa bei Bild- oder Sprachdaten der Fall ist.
Flexibilität und Komplexität
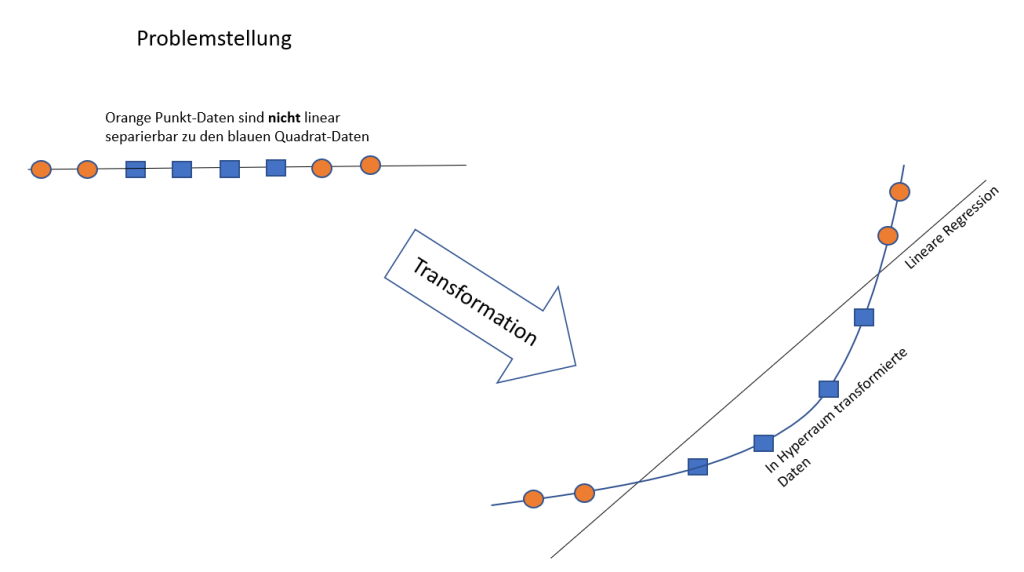
- SVM: Obwohl SVMs im Wesentlichen auf linearen Trennungen basieren, können sie mithilfe des sogenannten Kernel-Tricks auch nichtlineare Zusammenhänge modellieren. Der Kernel-Trick projiziert die Daten in einen höherdimensionalen Raum, in dem die Daten linear trennbar sind. Die häufig verwendeten Kernel wie der Radial Basis Function (RBF) Kernel ermöglichen es der SVM, komplexe Muster in den Daten zu erkennen, ohne dass explizit eine tiefe Netzwerkarchitektur erforderlich ist.
- Neuronale Netze: Neuronale Netze sind von Natur aus hochflexibel und in der Lage, sehr komplexe und tief verschachtelte Muster zu lernen. Sie bestehen aus mehreren Schichten von Neuronen (daher auch der Begriff „tiefe neuronale Netze“). Diese Tiefe ermöglicht es ihnen, hochkomplexe, nichtlineare Beziehungen in den Daten zu modellieren. Der Nachteil dieser Flexibilität ist jedoch, dass neuronale Netze oft lange Trainingszeiten erfordern und eine hohe Rechenleistung, insbesondere bei tiefen Netzwerken.
Erklärbarkeit und Transparenz
- SVM: Ein großer Vorteil von SVMs ist die Erklärbarkeit des Modells. Die Trennlinie, die das Modell wählt, kann oft relativ einfach visualisiert und verstanden werden, besonders bei linearen SVMs. Der Entscheidungsprozess der SVM basiert auf wenigen Datenpunkten (den Support-Vektoren), was die Transparenz erhöht.
- Neuronale Netze: Neuronale Netze gelten oft als Black-Box-Modelle, da es schwierig ist, genau nachzuvollziehen, wie die Entscheidung getroffen wird. Die vielen Schichten und Gewichte, die an der Entscheidungsfindung beteiligt sind, machen es schwer, das Modell und seine Vorhersagen zu interpretieren. Es gibt zwar Methoden wie LIME oder SHAP, um die Vorhersagen neuronaler Netze verständlicher zu machen, aber dies ist komplexer als bei SVMs.
Vor- und Nachteile von SVMs im Vergleich zu Neuronalen Netzen
Vorteile der SVM
- Gut geeignet für kleine, hochdimensionale Datensätze: SVMs funktionieren gut mit kleinen Datensätzen und sind besonders nützlich, wenn die Anzahl der Features hoch ist.
- Vermeidung von Overfitting: Durch den Maximierungsansatz des Margins kann die SVM gut generalisieren und neigt weniger dazu, sich zu stark an die Trainingsdaten anzupassen.
- Erklärbarkeit: Die Ergebnisse einer SVM sind oft intuitiver und leichter zu interpretieren als die von tiefen neuronalen Netzen.
Nachteile der SVM
- Skalierbarkeit: Bei sehr großen Datensätzen kann das Training einer SVM aufgrund der quadratischen Komplexität mit der Anzahl der Datenpunkte langsam werden.
- Begrenzte Flexibilität: Obwohl der Kernel-Trick SVMs flexibler macht, sind neuronale Netze oft besser darin, extrem komplexe nichtlineare Abhängigkeiten zu modellieren.
Fazit
Sowohl SVMs als auch neuronale Netze haben ihre Stärken und Schwächen, je nach Art des zu lösenden Problems. Eine SVM eignet sich besonders gut, wenn der Datensatz klein, hochdimensional und die Erklärbarkeit wichtig ist. Neuronale Netze hingegen sind ideal für große Datensätze und komplexe Muster, besonders wenn tiefe Strukturen benötigt werden, um die nichtlinearen Beziehungen in den Daten zu erkennen.
Der Einsatz hängt also stark von den Datenanforderungen, der Verfügbarkeit von Rechenressourcen und der Notwendigkeit der Interpretierbarkeit ab.
