Einleitung
In diesem Kapitel wird erklärt, wie Sie ein einfaches neuronales Netz von Grund auf selbst erstellen, ohne auf Bibliotheken wie TensorFlow wie im vorherigen Kapitel Einfaches KNN in Python (Tensorflow) zurückzugreifen. Stattdessen verwenden wir NumPy, um die wesentlichen Bausteine eines neuronalen Netzes selbst zu implementieren. Sie lernen, wie die Gewichte initialisiert, die Vorwärts- und Rückwärtspropagation durchgeführt und die Gewichte basierend auf dem Fehler angepasst werden. Dabei wird wieder das make_moons-Datenset aus sklearn verwendet, das sich gut als Beispiel für Klassifizierungsaufgaben eignet. Dieser Code eignet sich gut für eigene Modifikationen von neuronalen Netzen, welche mit Tensorflow nicht möglich sind (sie könnten z.B. ganz eigene Aktivierungsfunktionen erfinden oder versuchen rekurrente Verbindungen zu schaffen). In späteren Kapiteln werden wir allerdings immer wieder die Tensorflow-Bibliothek nutzen, da Sie bereits sehr viel Flexibilität bietet und den Programmieraufwand klein hält. Allerdings hilft die Erstellung eines eigenen neuronalen Netzes bei dem Verstehen wie sie funktionieren.
Das neuronale Netz besteht aus:
- Einer Eingabeschicht mit zwei Neuronen (da das
make_moons-Datenset zweidimensional ist), - Einer versteckten Schicht mit zehn Neuronen,
- Einer Ausgabeschicht mit einem Neuron für die binäre Klassifikation.
Das Ziel ist es, den „Mond“-förmigen Datensatz korrekt in zwei Klassen zu klassifizieren. Dieses Tutorial lässt sich einfach in Google Colab ausführen, was Ihnen die Möglichkeit gibt, den Code ohne lokale Installation auszuprobieren.
Voraussetzungen
Bevor Sie mit dem Code beginnen, benötigen Sie folgende Python-Bibliotheken:
- NumPy
- Scikit-learn (
sklearn)
Wenn Sie Google Colab verwenden, sind diese Pakete bereits vorinstalliert.
Überlegungen
Man könnte meinen dass jedes benötigte Neuron programmiert wird (z.B. als Klasse im objekt-orientierten Programmieren), allerdings finden bei näherer Betrachtung immer nur Matrix-Multiplikationen statt. Jedes Neuron auszuprogrammieren, würde den Code nur größer und die Ausführungsgeschwindigkeit reduzieren im Gegensatz zu einer abstrakteren Ausführung als Matrix-Multiplikationen.
Codeerläuterung
1. Import der Bibliotheken und Erstellung des Datensets
Zunächst importieren wir die notwendigen Bibliotheken und erzeugen unser Datenset:
import numpy as np
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
# Datenset erstellen
coord, cl = make_moons(300, noise=0.05)
X, Xt, y, yt = train_test_split(coord, cl, test_size=0.30, random_state=0)
Das make_moons-Datenset besteht aus zwei Klassen, die in einer halbmondförmigen Verteilung angeordnet sind. Mit train_test_split teilen wir die Daten in 70% Trainingsdaten und 30% Testdaten auf.
2. Initialisierung des neuronalen Netzes
Die Funktion zur Initialisierung der Gewichte verwendet die sogenannte He-Normalisierung, um zufällige, aber sinnvolle Startwerte für Gewichte zu erzeugen:
def init(inp, out):
return np.random.randn(inp, out) / np.sqrt(inp)
def createNN(inputLayer, firstLayer, outputLayer, randomSeed=0):
np.random.seed(randomSeed)
layers = X.shape[1], 3, 1
arch = list(zip(layers[:-1], layers[1:]))
weights = [init(inp, out) for inp, out in arch]
return weights
Die Funktion createNN erstellt die Struktur des neuronalen Netzes und initialisiert die Gewichtsmatrizen für jede Schicht. Die benötigte Anzahl der Neuronen der ersten Schicht wird selbstständig aus den Eingangsdaten abgeleitet (in unserem Fall 2, da es 2-Dimensionen der Punkte der Halbmonde gibt: x und y).
3. Aktivierungsfunktion und Feedforward-Propagation
Die Vorwärtspropagation mit der ReLU-Aktivierungsfunktion wird implementiert, um die Eingabedaten durch das Netz zu leiten:
def relu(z):
return np.maximum(0, z)
def reluDerivative(z):
return (z > 0).astype(float)
def feedForward(X, weights):
a = X.copy()
out = list()
for W in weights:
z = np.dot(a, W)
a = relu(z)
out.append(a)
return out
4. Rückwärtspropagation und Gewichtsaktualisierung
Die Rückwärtspropagation ermöglicht es, den Fehler über den Gradientenabstieg zu minimieren. Dies geschieht durch die Berechnung der Ableitung der ReLU-Funktion und die Anpassung der Gewichte, welche den Lernvorgang des neuronalen Netzes darstellen:
def backPropagation(l1, l2, weights, y):
l2Error = y.reshape(-1, 1) - l2
l2Delta = l2Error * reluDerivative(l2)
l1Error = l2Delta.dot(weights[1].T)
l1Delta = l1Error * reluDerivative(l1)
return l2Error, l1Delta, l2Delta
Die Gewichte werden basierend auf den Gradienten aktualisiert:
def updateWeights(X, l1, l1Delta, l2Delta, weights, alpha=1.0):
weights[1] = weights[1] + (alpha * l1.T.dot(l2Delta))
weights[0] = weights[0] + (alpha * X.T.dot(l1Delta))
return weights
5. Vorhersage und Genauigkeitsberechnung
Um Vorhersagen zu treffen und die Genauigkeit des Modells zu bewerten, verwenden wir folgende Funktionen:
def prediction(X, weights):
_, l2 = feedForward(X, weights)
preds = np.ravel((l2 > 0.5).astype(int))
return preds
def accuracy(trueLabel, predicted):
correctPreds = np.ravel(predicted) == trueLabel
return np.sum(correctPreds) / len(trueLabel)
6. Training des Netzes
Das neuronale Netz wird mit 2 Eingangsneuronen, 10 Neuronen in einer versteckten Schicht und einem Ausgangsneuron durch Aufruf der createNN()-Funktion erstellt.
Das neuronale Netz wird nun über 1000 Epochen trainiert, und alle 20 Epochen wird der Fehler sowie die Genauigkeit sowohl für das Training als auch für die Testdaten ausgegeben:
np.random.seed(0)
weights = createNN(X, 10, 1)
for i in range(1001): # 1000 epochs, including 0
l1, l2 = feedForward(X, weights)
l2Error, l1Delta, l2Delta = backPropagation(l1, l2, weights, y)
weights = updateWeights(X, l1, l1Delta, l2Delta, weights, alpha=0.01)
if (i % 20) == 0:
trainError = np.mean(np.abs(l2Error))
print('Epoche {:5}'.format(i), end=' - ')
print('Fehler: {:0.4f}'.format(trainError), end=' - ')
trainAccuracy = accuracy(trueLabel=y, predicted=(l2 > 0.5))
testPreds = prediction(Xt, weights)
testAccuracy = accuracy(trueLabel=yt, predicted=testPreds)
print('Genauigkeit: Training {:0.1f}%'.format(100*trainAccuracy), end=' | ')
print('Genauigkeit: Test {:0.1f}%'.format(100*testAccuracy))
Ausgabe
In der Ausgabe wird ersichtlich, dass das KNN am Anfang relativ schnell konvergiert, aber sich danach kaum noch verbessert:
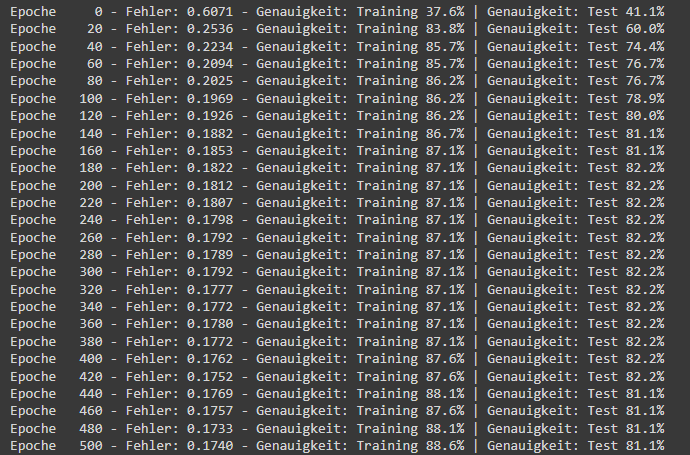
Zusammenfassung
In diesem Tutorial haben Sie gelernt, wie ein einfaches neuronales Netz von Grund auf mit NumPy erstellt und trainiert wird. Dieses Wissen ist eine solide Grundlage, um weiter in tiefere Netzwerke und komplexere Algorithmen einzutauchen. Es bietet zudem die Möglichkeit, mit verschiedenen Parametern wie der Netzstruktur, der Lernrate oder der Anzahl der Neuronen zu experimentieren, um die Genauigkeit weiter zu optimieren.
Probieren Sie den Code in Google Colab aus, um das Modell zu trainieren und zu testen!
Im nächsten Kapitel Erkennung von handgeschriebenen Zahlen sehen wir uns ein erstes reales Beispiel für eine Klassifikation von Bildern durch neuronale Netze an.
Kompletter Code (zum einfacheren Kopieren):
import numpy as np
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
def init(inp, out):
return np.random.randn(inp, out) / np.sqrt(inp)
def createNN(inputLayer, firstLayer,
outputLayer, randomSeed=0):
np.random.seed(randomSeed)
layers = X.shape[1], 3, 1
arch = list(zip(layers[:-1], layers[1:]))
weights = [init(inp, out) for inp, out in arch]
return weights
def relu(z):
return np.maximum(0, z)
def reluDerivative(z):
return (z > 0).astype(float)
def feedForward(X, weights):
a = X.copy()
out = list()
for W in weights:
z = np.dot(a, W)
a = relu(z)
out.append(a)
return out
def accuracy(trueLabel, predicted):
correctPreds = np.ravel(predicted) == trueLabel
return np.sum(correctPreds) / len(trueLabel)
def backPropagation(l1, l2, weights, y):
l2Error = y.reshape(-1, 1) - l2
l2Delta = l2Error * reluDerivative(l2)
l1Error = l2Delta.dot(weights[1].T)
l1Delta = l1Error * reluDerivative(l1)
return l2Error, l1Delta, l2Delta
def updateWeights(X, l1, l1Delta, l2Delta, weights, alpha=1.0):
weights[1] = weights[1] + (alpha * l1.T.dot(l2Delta))
weights[0] = weights[0] + (alpha * X.T.dot(l1Delta))
return weights
def prediction(X, weights):
_, l2 = feedForward(X, weights)
preds = np.ravel((l2 > 0.5).astype(int))
return preds
np.random.seed(0)
coord, cl = make_moons(300, noise=0.05)
X, Xt, y, yt = train_test_split(coord, cl,
test_size=0.30,
random_state=0)
weights = createNN(X, 10, 1)
for i in range(1001): # 1000 epochs, including 0
l1, l2 = feedForward(X, weights)
l2Error, l1Delta, l2Delta = backPropagation(l1, l2, weights, y)
weights = updateWeights(X, l1, l1Delta, l2Delta, weights, alpha=0.01)
if (i % 20) == 0:
trainError = np.mean(np.abs(l2Error))
print('Epoche {:5}'.format(i), end=' - ')
print('Fehler: {:0.4f}'.format(trainError), end= ' - ')
trainAccuracy = accuracy(trueLabel=y, predicted=(l2 > 0.5))
testPreds = prediction(Xt, weights)
testAccuracy = accuracy(trueLabel=yt, predicted=testPreds)
print('Genauigkeit: Training {:0.1f}%'.format(100*trainAccuracy), end= ' | ')
print('Genauigkeit: Test {:0.1f}%'.format(100*testAccuracy))
