Neuronales Netz mit TensorFlow/Keras in Google Colab – Ein einfaches Tutorial
In diesem Tutorial zeige ich, wie man mit wenigen Zeilen Code in Google Colab ein neuronales Netz erstellt und trainiert. Aber keine Sorge, wir halten es hier ganz einfach und das hiergewählte Beispiel ist an den Tensorflow Playground angelehnt, den wir im vorherigen Kapitel angesehen haben.
Am Ende des Tutorials soll jeder in der Lage sein, ein kleines, aber funktionierendes Beispiel eines neuronalen Netzes zu verstehen und selbst zu erstellen. Wir konzentrieren uns auf die wesentlichen Teile und erklären sie so verständlich wie möglich.
1. Los geht’s
Neuronale Netze lernen, Muster in Daten zu erkennen. In unserem Beispiel verwenden wir einen Spielzeug-Datensatz, der aus zwei Gruppen von Punkten besteht, die wie zwei Halbmonde aussehen, damit wir etwas zum Nutzen des neuronalen Netzes haben.
Das Ziel des neuronalen Netzes ist es, zu lernen, ob ein Punkt zu dem einen oder dem anderen Halbmond gehört.
Diese zwei Gruppen von Punkten nennen wir Klassen. Ein Punkt gehört entweder zur ersten Klasse oder zur zweiten Klasse – und das Netz soll lernen, das zu entscheiden.
2. Die Umgebung und die Daten vorbereiten
Damit wir das neuronale Netz nutzen können, müssen wir zuerst einige Dinge vorbereiten: Die nötigen Bibliotheken und die Daten, mit denen das Netz lernen soll.
Bibliotheken importieren
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
import tensorflow as tf
from tensorflow.keras import layers
from matplotlib.colors import ListedColormap
from IPython.display import clear_output
- NumPy und Matplotlib: Helfen uns, die Daten zu erzeugen und die Ergebnisse zu visualisieren.
- Scikit-Learn: Eine nützliche Bibliothek, die uns dabei hilft, Trainingsdaten zu erstellen.
- TensorFlow/Keras: Unsere Hauptbibliothek für neuronale Netze. Diese stammt von Google und ist einerseits leicht zu bedienen und gleichzeit sehr flexibel um z.B. größere, komplexere Arbeiten mit neuronalen Netzen zu stemmen oder eigene Änderung an neuronalen Netzen vorzunehmen und die Reaktion darauf zu erforschen.
Den Datensatz erstellen
Wir erzeugen die Punkte, die unser neuronales Netz lernen soll, zu unterscheiden.
# Generiere die Moons-Daten (Halbmonde)
X, y = make_moons(n_samples=300, noise=0.05, random_state=42)
y = y.reshape(-1, 1)
Hier erzeugen wir 300 Punkte, die in zwei Gruppen (die „Halbmonde“) aufgeteilt sind. Diese Gruppen simulieren eine reale Situation, bei der man zwei unterschiedliche Dinge erkennen will. Von beiden Gruppen (rot und blau) gibt es je zwei bekannte Größen – dargestellt auf der x- und y-Achse. Wie man sieht lassen sich die beiden Gruppen nicht linear trennen, also nicht durch einen linearen „Strich“. Stattdessen wird eine komplexere Separierung wie z.B. eine horizonal liegende S-förmige Linie benötigt, die das neuronale Netz lernen soll.
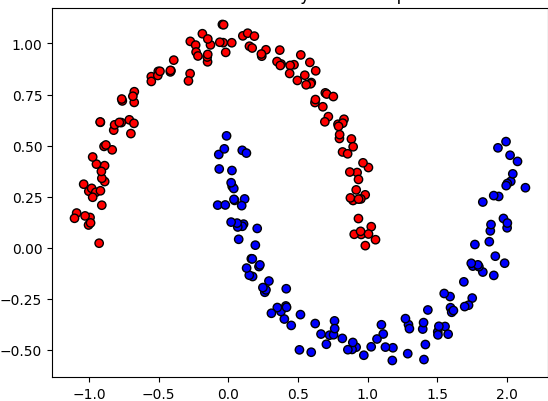
Als Mensch ist dieses Bild natürlich sehr einfach und wir könnten mit einem einfachen Pinselstrich eine Separierungslinie einzeichnen. Dies geht allerdings nur bei so einfachen Beispielen, bei denen wir nur zwei Dimensionen (x- und y-Achse haben). Bei der Separierung von z.B. Hundephotos von Katzenphotos hätten wir allerdings ähnlich viele Dimensionen wie Pixel in den Photos, d.h. Tausende oder sogar Millionen Dimensionen. Diese lassen sich weder graphisch darstellen noch könnte ein Mensch hier einfach eine Separierungslinie zeichnen (wobei es hier eher Separierungsflächen, genau genommen sogar Separierungshyperflächen wären). So hochdimensionale Separierungsprobleme sind allerdings für neuronale Netze genauso gut lösbar wie unser zweidimensionales Beispiel – es benötigt „lediglich“ mehr Neuronen in den Netzwerken und ggf. mehr Lernschritte.
Die Daten vorbereiten
Damit das Netz besser arbeiten kann, müssen wir die Daten in einer bestimmten Form bereitstellen:
# One-Hot-Encoding für die Labels (Daten aufbereiten)
encoder = OneHotEncoder(sparse_output=False)
y = encoder.fit_transform(y)
# Aufteilen in Trainings- und Testdaten
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
- One-Hot-Encoding: Wir bereiten die Daten so vor, dass das Netz gut mit ihnen arbeiten kann. Hier sagen wir, dass jeder Punkt zu einer der beiden Klassen gehört (Halbmond 1 oder Halbmond 2).
- Trainings- und Testdaten: Die Daten werden in zwei Teile geteilt: Ein Teil wird zum Trainieren des Netzes verwendet, der andere, um zu prüfen, wie gut das Netz gelernt hat.
3. Ein einfaches neuronales Netz erstellen
Jetzt wird’s spannend! Wir erstellen unser neuronales Netz – das Herzstück des Ganzen. Mit Keras können wir das Netz sehr einfach definieren.
# Modell definieren
model = tf.keras.Sequential([
layers.Input(shape=(2,)), # 2 Input-Neuronen (für die Koordinaten x und y)
layers.Dense(8, activation='relu'), # 8 Neuronen in der versteckten Schicht
layers.Dense(2, activation='softmax') # 2 Output-Neuronen (für die 2 Klassen)
])
Was passiert hier?
- Input-Schicht: Das Netz erhält zwei Werte als Eingabe (x- und y-Koordinate eines Punktes).
- Versteckte Schicht: Diese Schicht hat 8 Neuronen. Sie lernt, komplizierte Zusammenhänge zwischen den Eingaben zu erkennen. Sie können hier einfach eine größere Zahl eingeben um mehr Neuronen in der versteckten Schicht zu generieren. Oder sie dupplizieren die Zeile und erhalten eine zweite versteckte Schicht mit 8 Neuronen.
- Ausgabeschicht: Diese Schicht entscheidet, zu welcher Klasse (Halbmond 1 oder Halbmond 2) ein Punkt gehört.
Das Modell bereit machen
Bevor wir das Netz trainieren können, müssen wir es „kompilieren“. Dabei sagen wir dem Netz, wie es lernen soll.
# Kompiliere das Modell
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
Adam-Optimizer: Er sorgt dafür, dass das Netz seine Fehler im Laufe der Zeit minimiert.
Loss (Fehlerfunktion): Hier messen wir, wie gut oder schlecht das Netz arbeitet.
Metrics: Wir wollen sehen, wie genau das Netz die Klassen vorhersagt.
4. Training und Visualisierung
Nun trainieren wir das neuronale Netz und lassen es dabei immer wieder zeigen, wie es sich verbessert. Wir visualisieren das Ganze, damit klar wird, wie das Netz lernt, die Punkte zu trennen. Dies ist ebenso wie die Moons-Trainingsdatengenerierung kein Schritt, den man braucht um ein neuronales Netz zu erstellen. Sondern lediglich um den Lernfortschritt darzustellen (man beachte, dass die Erstellung des neuronalen Netzes obenstehend „weniger Code“ benötigt als die Erzeugung der Trainingsdaten oder das Plotten des Lernfortschrittes).
# Anzahl der Epochen und Intervalle zum Plotten
epochs = 1000
plot_interval = 10 # Alle 10 Epochen soll das Diagramm aktualisiert werden
# Generiere ein Gitter für die Entscheidungsgrenzen
x_min, x_max = X_train[:, 0].min() - 0.5, X_train[:, 0].max() + 0.5
y_min, y_max = X_train[:, 1].min() - 0.5, X_train[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
# Schleife über die Epochen und schrittweises Training
for epoch in range(0, epochs, plot_interval):
# Trainiere für 'plot_interval' Epochen
model.fit(X_train, y_train, epochs=plot_interval, batch_size=32, verbose=0)
# Vorhersagen für das Gitter
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = np.argmax(Z, axis=1)
Z = Z.reshape(xx.shape)
# Lösche den aktuellen Inhalt der Achse und plotte neu
clear_output(wait=True)
# Plotte die Entscheidungsgrenzen
plt.contourf(xx, yy, Z, alpha=0.8, cmap=ListedColormap(('red', 'blue')))
plt.scatter(X_train[:, 0], X_train[:, 1], c=np.argmax(y_train, axis=1), edgecolors='k', marker='o', cmap=ListedColormap(('red', 'blue')))
plt.title(f'Decision Boundary after {epoch + plot_interval} Epochs')
plt.show()
- Epochs („Trainingsrunden“ oder „Lernrunden“): Dies ist die Anzahl der Durchgänge, die das Netz durchläuft, um die Daten zu lernen.
- Plotten: Nach jeder festgelegten Anzahl von Epochen zeigen wir die Fortschritte, indem wir die Grenze zwischen den zwei Gruppen von Punkten (Klassen) visualisieren.
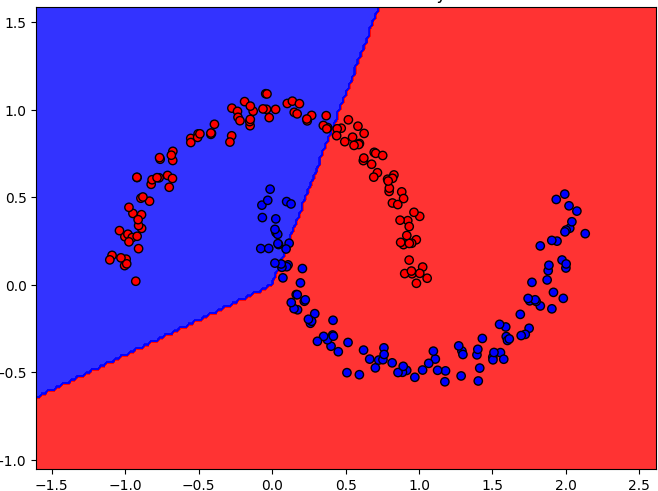
Die Flächen zeigen an, wie das neuronale Netz vor dem Training mit seinen zufällig gewählten Neuronengewichte, Punkte zuordnen würde. Wir sehen, dass die meisten Punkte der zwei Halbmonde den falschen Klassen bzw. Farben zugeordnet werden – dies soll sich durch das Training des neuronalen Netzes ändern.
Das Endergebnis plotten
Nachdem das neuronale Netz über z.B. 1000 Epochen trainiert wurde, sollte es in der Lage sein, Punkte korrekt dem jeweiligen Halbmond bzw. Farbe zuzuordnen.
Am Ende plotten wir die endgültige Entscheidungsgrenze, die zeigt, wie gut das Netz gelernt hat, die zwei Gruppen zu trennen.
# Finaler Plot der Entscheidungsgrenze nach dem Training
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = np.argmax(Z, axis=1)
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.8, cmap=ListedColormap(('red', 'blue')))
plt.scatter(X_train[:, 0], X_train[:, 1], c=np.argmax(y_train, axis=1), edgecolors='k', marker='o', cmap=ListedColormap(('red', 'blue')))
plt.title('Final Decision Boundary')
plt.show()
Wenn Sie den Code ausführen und mehrere hundert Epochen, sollten Sie sehen, dass das Training erfolgreich war. Dies erkennen Sie daran, dass die Farbflächen die jeweilig gleichfarbigen Punkte umschließen. Die Grenzen zwischen den Farbflächen sind nun die vom neuronalen Netz ermittelten Klassengrenzen. Jeder neue Punkt, den Sie in einem realen Szenario später ermitteln und durch das neuronale Netz klassifizieren lassen würden, würde gemäß der Farbflächen eingeordnet werden.
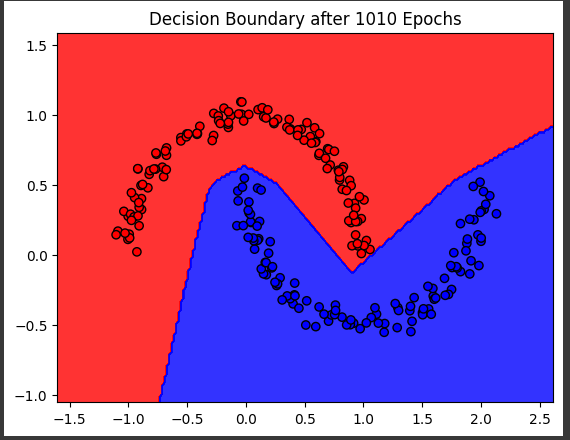
Der Screenshot zeigt, dass nun das neuronale Netz die Punkte korrekt klassifiziert. Ihr Plot zeigt vermutlich andere Klassengrenzen (bzw. andere Grenzen der beiden Farbflächen) – dies resultiert daraus, dass das neuronale Netz mit zufällig gewählten Neuronengewichte gestartet ist. D.h. Ihr initiales Netz war anders parametriert als das hier dargestellte, welches sich in einem leicht anderen Endergebnis widerspiegelt.
Vielleicht stellen Sie auch fest, dass das neuronale Netz zwar die dargestellten Punkte einwandfrei klassifzieren kann, aber außerhalb der Punktewolke unsymmetrische oder sogar komische Grenzen zieht. Dies ist tatsächlich eine Limitierung von neuronalen Netzen: Während Interpolation meist gut funktioniert, klappt es bei Extrapolation häufig nicht mehr so gut. D.h. wenn Sie weitere blaue Punkte leicht außerhalb des blauen Halbmondes hinzufügen würden, die z.B. die Werte x=2.0 und y=0.7 haben, würden diese vom neuronalen Netz fälschlich als „rot“ kategoriert. Als Mensch würden wir diesen Punkt aber an Hand der Visualisierung eher dem blauen Halbmond zuordnen. Diese Systemgrenze sollte man beim Training und Nutzung immer bedenken, insbesondere wenn es keine so schöne zweidimensionale Darstellung gibt, sondern sich alles in abstrakteren, nicht visualisierbaren höherdimensionalen Entscheidungsräumen abspielt.
Im nächsten Kapitel Ein selbst erstelltes Neuronales Netz lernen Sie wie Sie ein neuronales Netz sogar ohne spezielle KNN-Libraries (wie Tensorflow) erstellen können.
5. Gesamter Code
Mit nur wenigen Zeilen Code können Sie ein neuronales Netz in Google Colab erstellen und trainieren. Es ist faszinierend, wie einfach es ist, diese leistungsstarke Technologie mit TensorFlow und Keras zu nutzen. Dieses Beispiel zeigt, wie das Netz zwei Gruppen von Punkten unterscheidet – ein Konzept, das auf viele reale Probleme angewendet werden kann.
Hier sei noch der gesamte Code gezeigt – kopieren Sie ihn gerne in Ihre Python-Umgebung bzw. in Colab:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
import tensorflow as tf
from tensorflow.keras import layers
from matplotlib.colors import ListedColormap
from IPython.display import clear_output
# Generiere die Moons-Daten
X, y = make_moons(n_samples=300, noise=0.05, random_state=42)
y = y.reshape(-1, 1)
# One-Hot-Encoding für die Labels
encoder = OneHotEncoder(sparse_output=False)
y = encoder.fit_transform(y)
# Aufteilen in Trainings- und Testdaten
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Modell definieren
model = tf.keras.Sequential([
layers.Input(shape=(2,)), # 2 Input-Neuronen
layers.Dense(8, activation='relu'), # 4 Neuronen in der versteckten Schicht
layers.Dense(2, activation='softmax') # 2 Output-Neuronen (für die 2 Klassen)
])
# Kompiliere das Modell
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
# Anzahl der Epochen und Intervalle zum Plotten
epochs = 1000
plot_interval = 10 # Alle 10 Epochen soll das Diagramm aktualisiert werden
# Initialisiere das Diagramm nur einmal
plt.figure(figsize=(8, 6))
# Generiere ein Gitter für die Entscheidungsgrenzen
x_min, x_max = X_train[:, 0].min() - 0.5, X_train[:, 0].max() + 0.5
y_min, y_max = X_train[:, 1].min() - 0.5, X_train[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
np.arange(y_min, y_max, 0.02))
# Finaler Plot der Entscheidungsgrenze nach dem Training
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = np.argmax(Z, axis=1)
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.8, cmap=ListedColormap(('red', 'blue')))
plt.scatter(X_train[:, 0], X_train[:, 1], c=np.argmax(y_train, axis=1), edgecolors='k', marker='o', cmap=ListedColormap(('red', 'blue')))
plt.title('Final Decision Boundary')
plt.show()
# Schleife über die Epochen und schrittweises Training
for epoch in range(0, epochs, plot_interval):
# Trainiere für 'plot_interval' Epochen ohne Callbacks
model.fit(X_train, y_train, epochs=plot_interval, batch_size=32, verbose=0)
# Vorhersagen für das Gitter
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = np.argmax(Z, axis=1)
Z = Z.reshape(xx.shape)
# Lösche den aktuellen Inhalt der Achse und plotte neu
clear_output(wait=True)
# Plotte die Entscheidungsgrenzen
plt.contourf(xx, yy, Z, alpha=0.8, cmap=ListedColormap(('red', 'blue')))
# Plotte die Trainingsdaten
plt.scatter(X_train[:, 0], X_train[:, 1], c=np.argmax(y_train, axis=1), edgecolors='k', marker='o', cmap=ListedColormap(('red', 'blue')))
# Setze den Titel des Plots
plt.title(f'Decision Boundary after {epoch + plot_interval} Epochs')
# Zeige das aktualisierte Diagramm
plt.show()
# Finaler Plot der Entscheidungsgrenze nach dem Training
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = np.argmax(Z, axis=1)
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, alpha=0.8, cmap=ListedColormap(('red', 'blue')))
plt.scatter(X_train[:, 0], X_train[:, 1], c=np.argmax(y_train, axis=1), edgecolors='k', marker='o', cmap=ListedColormap(('red', 'blue')))
plt.title('Final Decision Boundary')
plt.show()
